K čemu se používají epicyklické převody？

Epicyklické převodyTaké známé jako planetové převodovky, jsou široce používány v různých průmyslových odvětvích díky své kompaktní konstrukci, vysoké účinnosti a všestrannosti.

Tyto převody se používají především v aplikacích, kde je omezený prostor, ale je nezbytný vysoký točivý moment a variabilita otáček.

1. Automobilové převodovky: Epicyklické převody jsou klíčovou součástí automatických převodovek, které zajišťují plynulé řazení, vysoký točivý moment při nízkých rychlostech a efektivní přenos výkonu.
2. Průmyslové stroje: Používají se v těžkých strojích pro svou schopnost zvládat vysoké zatížení, rovnoměrně rozkládat točivý moment a efektivně pracovat v kompaktních prostorech.
3. Letectví a kosmonautika: Tato ozubená kola hrají klíčovou roli v leteckých motorech a rotorech vrtulníků, což zajišťuje spolehlivost a přesné řízení pohybu za náročných podmínek.
4. Robotika a automatizace: V robotice se planetové převody používají k dosažení přesného řízení pohybu, kompaktní konstrukce a vysokého točivého momentu v omezených prostorech.

Jaké jsou čtyři prvky planetového ozubeného kola?

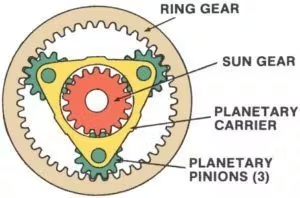
Epicyklické soukolí, známé také jakoplanetové převodovky Systém je vysoce účinný a kompaktní mechanismus běžně používaný v automobilových převodovkách, robotice a průmyslových strojích. Tento systém se skládá ze čtyř klíčových prvků:

1. Sluneční převodovkaCentrální kolo, umístěné uprostřed soukolí, je primárním hnací silou neboli přijímačem pohybu. Je v přímém záběru s planetovými koly a často slouží jako vstup nebo výstup systému.

2. Planetová převodovkaJedná se o několik ozubených kol, která se otáčejí kolem centrálního kola. Jsou namontována na nosiči planetových kol a zabírají jak s centrálním kolem, tak s korunovým kolem. Planetová kola rovnoměrně rozkládají zatížení, díky čemuž je systém schopen zvládat vysoký točivý moment.

3.Planetární nosičTato součást drží planetová kola na místě a podporuje jejich rotaci kolem centrálního kola. Unášeč planet může v závislosti na konfiguraci systému fungovat jako vstupní, výstupní nebo stacionární prvek.

4.Ozubený věnecJedná se o velké vnější ozubené kolo, které obklopuje planetová kola. Vnitřní zuby korunového kola zabírají s planetovými koly. Stejně jako ostatní prvky může korunové kolo sloužit jako vstup, výstup nebo zůstat nehybné.

Souhra těchto čtyř prvků poskytuje flexibilitu pro dosažení různých rychlostních poměrů a změn směru v rámci kompaktní struktury.

Jak vypočítat převodový poměr v planetovém soukolí?

Převodový poměrplanetové soukolí záleží na tom, které komponenty jsou pevné, vstupní a výstupní. Zde je podrobný návod k výpočtu převodového poměru:

1. Pochopte konfiguraci systému:

Určete, který prvek (Slunce, nosič planety nebo prstenec) je stacionární.

Určete vstupní a výstupní složky.

2. Použijte základní rovnici pro převodový poměr: Převodový poměr planetového převodu lze vypočítat pomocí:

GR = 1 + (R / S)

Kde:

GR = Převodový poměr

R = Počet zubů na ozubeném věnci

S = Počet zubů na centrálním kole

Tato rovnice platí, když je výstupem unašeč planetového kola a buď centrální kolo, nebo korunové kolo je v klidu.

3. Úprava pro další konfigurace:

• Pokud je centrální kolo v klidu, výstupní otáčky systému jsou ovlivněny převodovým poměrem korunového kola a unašeče planetového kola.
• Pokud je ozubený věnec nehybný, výstupní otáčky jsou určeny vztahem mezi centrálním kolem a nosičem planetových kol.

4. Zpětný převodový poměr pro výstup a vstup: Při výpočtu snížení rychlosti (vstup vyšší než výstup) je poměr přímočarý. Pro násobení rychlosti (výstup vyšší než vstup) invertujte vypočítaný poměr.

Příklad výpočtu:

Předpokládejme, že soukolí má:

Ozubený věnec (R): 72 zubů

Centrální ozubené kolo (S): 24 zubů

Pokud je unašeč planetových kol výstupní a centrální kolo je nehybné, převodový poměr je:

GR = 1 + (72/24) GR = 1 + 3 = 4

To znamená, že výstupní rychlost bude 4krát nižší než vstupní rychlost, což poskytuje redukční poměr 4:1.

Pochopení těchto principů umožňuje inženýrům navrhovat efektivní a všestranné systémy přizpůsobené specifickým aplikacím.