Planetový převod se jako převodový mechanismus široce používá v různých inženýrských postupech, jako jsou reduktory, jeřáby, planetové reduktory atd. Planetový převod může v mnoha případech nahradit převodový mechanismus pevného ozubeného soukolí. Protože proces převodu ozubeného soukolí je liniový kontakt, dlouhodobé zapojení způsobí selhání ozubeného kola, proto je nutné simulovat jeho pevnost. Li Hongli a kol. použili metodu automatického zapojení k zapojení planetového převodu a zjistili, že krouticí moment a maximální napětí jsou lineární. Wang Yanjun a kol. také zapojili planetové převodovku do sítě metodou automatického generování a simulovali statickou a modální simulaci planetového převodu. V tomto článku se k rozdělení sítě používají hlavně tetraedrové a hexaedrové prvky a konečné výsledky jsou analyzovány, aby se zjistilo, zda jsou splněny pevnostní podmínky.

1. Vytvoření modelu a analýza výsledků

Trojrozměrné modelování planetového převodu

Planetové převodovkyse skládá hlavně z ozubeného věnce, centrálního kola a planetového kola. Hlavní parametry vybrané v tomto článku jsou: počet zubů vnitřního ozubeného věnce je 66, počet zubů centrálního kola je 36, počet zubů planetového kola je 15, vnější průměr vnitřního ozubeného věnce je 150 mm, modul je 2 mm, úhel tlaku je 20 °, šířka zubu je 20 mm, součinitel výšky nástavce je 1, součinitel vůle je 0,25 a existují tři planetová kola.

Statická simulační analýza planetového převodu

Definujte vlastnosti materiálu: importujte trojrozměrný planetový převodový systém nakreslený v softwaru UG do ANSYS a nastavte parametry materiálu, jak je uvedeno v tabulce 1 níže:

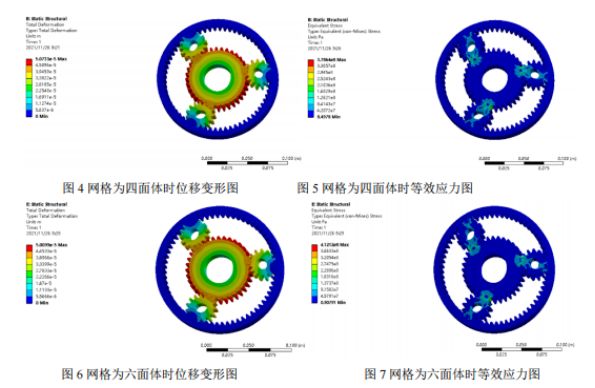
Síťování: Síť konečných prvků je rozdělena tetraedrem a hexaedrem a základní velikost prvku je 5 mm. Protožeplanetové převodovky, centrální kolo a vnitřní ozubený věnec jsou v kontaktu a záběru, síť kontaktních a síťových částí je zhuštěna a její velikost je 2 mm. Nejprve se použijí tetraedrické mřížky, jak je znázorněno na obrázku 1. Celkem se vygeneruje 105 906 prvků a 177 893 uzlů. Poté se použije hexaedrická mřížka, jak je znázorněno na obrázku 2, a celkem se vygeneruje 26 957 buněk a 140 560 uzlů.

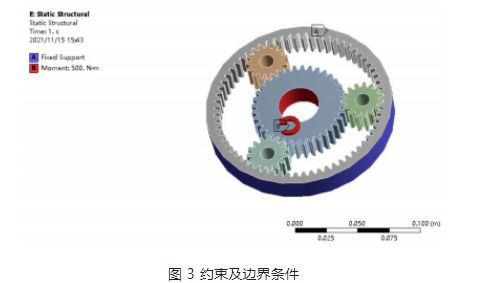
Aplikace zatížení a okrajové podmínky: podle pracovních charakteristik planetového kola v reduktoru je centrální kolo hnacím kolem, planetové kolo hnaným kolem a konečný výstup je přes unašeč planet. Upevněte vnitřní ozubený věnec v programu ANSYS a na centrální kolo aplikujte krouticí moment 500 N·m, jak je znázorněno na obrázku 3.

Následné zpracování a analýza výsledků: Níže jsou uvedeny nefogramy posunutí a ekvivalentního nefogramu napětí získané statickou analýzou ze dvou dělení mřížky a je provedena srovnávací analýza. Z nefogramů posunutí obou typů mřížek vyplývá, že k maximálnímu posunutí dochází v poloze, kde centrální kolo nezabírá s planetovým kolem, a k maximálnímu napětí dochází v patě záběru ozubeného kola. Maximální napětí v tetraedrické mřížce je 378 MPa a maximální napětí v hexaedrické mřížce je 412 MPa. Vzhledem k tomu, že mez kluzu materiálu je 785 MPa a součinitel bezpečnosti je 1,5, je přípustné napětí 523 MPa. Maximální napětí v obou výsledcích je menší než přípustné napětí a oba splňují pevnostní podmínky.

2. Závěr

Prostřednictvím simulace planetového převodu metodou konečných prvků je získán nefogram posuvné deformace a nefogram ekvivalentního napětí převodového systému, ze kterých jsou vypočítány maximální a minimální data a jejich rozložení vplanetové převodovkymodel lze nalézt. Místo maximálního ekvivalentního napětí je také místem, kde je největší pravděpodobnost selhání zubů ozubeného kola, proto je třeba mu během návrhu nebo výroby věnovat zvláštní pozornost. Analýzou celého systému planetového převodu se překonává chyba způsobená analýzou pouze jednoho zubu ozubeného kola.